Difference between revisions of "Ranunculus occidentalis"
| (21 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ''''' | + | *Scientific Name: ''Ranunculus occidentalis'' var. ''occidentalis'' |
| − | + | * Family: Ranunculaceae | |
| − | + | * Common Names: western buttercup | |
| + | * Synonyms/Misapplications: ''Ranunclus eisenii, R. occidentalis'' var''. eisenii, R. o.'' var. ''rattanii, R. o.'' var. ''typicus'' | ||
| + | * Codon: RANOCC | ||
| + | ---- | ||
| + | [[File:RAOC BenLegler veg avg.jpg|thumb|photo by Ben Legler]] | ||
| + | === Taxonomy === | ||
{{Taxobox | {{Taxobox | ||
| − | | name = | + | | name = |
| − | + | | regnum = [[Plant]]ae | |
| − | + | | subregnum = Viridiplantae | |
| − | | regnum = | + | | phylum = Tracheophyta |
| − | | subregnum = | + | | subphylum= Spermatophytina |
| − | | phylum = | + | |
| − | | subphylum= | + | |
| classis = Magnoliopsida | | classis = Magnoliopsida | ||
| − | | subclassis = | + | | subclassis = Ranunculanae |
| ordo = Ranunculales | | ordo = Ranunculales | ||
| familia = Ranunculaceae | | familia = Ranunculaceae | ||
| − | | genus = '''''Ranunculus''''' | + | | genus = ''Ranunculus'' L. |
| − | | | + | | species = '''''Ranunculus occidentalis''''' Nutt. |
| − | | | + | | subspecies = '''''Ranunculus occidentalis'' var. ''occidentalis''''' Nutt. |
| − | | | + | | range_map = |
| − | + | | range_map_caption = | |
| − | + | ||
}} | }} | ||
| + | <ref>Integrated Taxonomic Information System. Retrieved from https://www.itis.gov/servlet/SingleRpt/SingleRpt?search_topic=TSN&search_value=18632#null</ref> | ||
| − | |||
===Description=== | ===Description=== | ||
| − | + | Erect perennial with stiff hairs emerging from slender fibrous roots, stems usually hollow, 1.5-4 dm tall. | |
| − | + | ||
| − | + | ||
| + | Basal leaves long-petiolate, the blades 2-3.5 cm. long, deeply lobed into 3 segments, the lobes with coarse, rounded teeth; cauline leaves alternate, more deeply dissected, reduced upward to the entire bracts. | ||
| + | Sepals strongly reflexed along a well-defined fold, bears 5-petaled yellow flowers with many pistils. | ||
| + | |||
| + | The fruit is an aggregate of pumpkin-seed shaped achenes. The styles jutting out from the ends of achenes are less hooked than ''R. uncinatus.'' Leaves are also more pubescent and lighter in color than ''R. uncinatus.''<ref>WTU Herbarium, Burke Museum, & University of Washington. Retrieved from <nowiki>https://biology.burke.washington.edu/herbarium/imagecollection/taxon.php?Taxon=Ranunculus%20occidentalis%20var.%20occidentalis</nowiki></ref><ref name=":1">Hitchcock, C. L., Cronquist, A., Giblin, D., & Legler, | ||
| + | B. et al. (2018). ''Flora of the Pacific Northwest: an illustrated manual''. | ||
| + | Seattle: University of Washington Press.</ref><ref name=":0" /> | ||
===Bloom Period=== | ===Bloom Period=== | ||
| − | April-June <ref name=" | + | [[File:RAOC distribution.png|300px|thumb|right|''Ranunculus occidentalis'' range]] |
| + | April-June, right before and among the Camas.<ref name=":0">Bowcutt, F., & Hamman, Sarah. (2016). ''Vascular plants'' | ||
| + | of the South Sound prairies'' (First ed.). Olympia, Washington: The Evergreen'' | ||
| + | State College Press.</ref> | ||
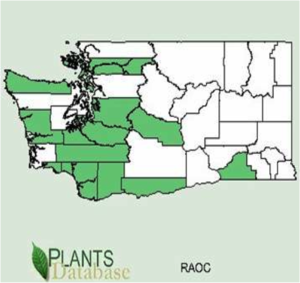
===Distribution=== | ===Distribution=== | ||
| − | + | Southwest BC south, west of the Cascades, and in Columbia River Gorge, to California.<ref name=":1" /> | |
| − | + | ||
| − | + | ||
===Habitat=== | ===Habitat=== | ||
| − | Moist to well-drained soil, | + | Moist to well-drained soil, meadows and open woods, mostly west Cascades, Alaska to California, east to Alberta and northeast Oregon.<ref name=":1" /> |
| − | <ref name=" | + | |
===Uses=== | ===Uses=== | ||
| − | + | Ecological: Adult Mardon Skippers (''Polites mardon'') feed on the nectar of ''R. occidentalis,'' among other flowers. <ref name=":0" /> | |
| − | + | ||
| − | = | + | First Nations: The juice from the flowers used as a poison. Seeds cooked and used as piñole either on their own or mixed with other seeds. The seed must be parched in order to remove an acrid principle.<ref>Native American Ethnobotany Database. Retrieved from <nowiki>http://naeb.brit.org/uses/search/?string=ranunculus+occidentalis</nowiki></ref> |
| Line 51: | Line 56: | ||
===Seed=== | ===Seed=== | ||
| − | [[File:Ranunculus occidentalis.jpg|300px|thumb|right| | + | [[File:Ranunculus occidentalis.jpg|300px|thumb|right|Lisa Hintz]] |
| − | + | ||
'''Seed sample from:''' 2011 | '''Seed sample from:''' 2011 | ||
| Line 79: | Line 83: | ||
===Photo Gallery=== | ===Photo Gallery=== | ||
<gallery> | <gallery> | ||
| − | File: | + | File:RANOCC2.jpg|photo by Ben Legler |
| − | File: | + | File:RANOCC1.jpg|young growth, courtesy of CNLM |
| − | File:Ranunculus occidentalis.jpg | + | File:Ranunculus occidentalis.jpg| Lisa Hintz |
</gallery> | </gallery> | ||
| + | |||
===References=== | ===References=== | ||
| − | < | + | <references /> |
Latest revision as of 23:38, 20 March 2021
- Scientific Name: Ranunculus occidentalis var. occidentalis
- Family: Ranunculaceae
- Common Names: western buttercup
- Synonyms/Misapplications: Ranunclus eisenii, R. occidentalis var. eisenii, R. o. var. rattanii, R. o. var. typicus
- Codon: RANOCC
Contents
Taxonomy
| Scientific classification | |
|---|---|
| Kingdom: | Plantae |
| Subkingdom: | Viridiplantae |
| Phylum: | Tracheophyta |
| Subphylum: | Spermatophytina |
| Class: | Magnoliopsida |
| Subclass: | Ranunculanae |
| Order: | Ranunculales |
| Family: | Ranunculaceae |
| Genus: | Ranunculus L. |
| Species: | Ranunculus occidentalis Nutt. |
| Subspecies: | Ranunculus occidentalis var. occidentalis Nutt. |
Description
Erect perennial with stiff hairs emerging from slender fibrous roots, stems usually hollow, 1.5-4 dm tall.
Basal leaves long-petiolate, the blades 2-3.5 cm. long, deeply lobed into 3 segments, the lobes with coarse, rounded teeth; cauline leaves alternate, more deeply dissected, reduced upward to the entire bracts.
Sepals strongly reflexed along a well-defined fold, bears 5-petaled yellow flowers with many pistils.
The fruit is an aggregate of pumpkin-seed shaped achenes. The styles jutting out from the ends of achenes are less hooked than R. uncinatus. Leaves are also more pubescent and lighter in color than R. uncinatus.[2][3][4]
Bloom Period
April-June, right before and among the Camas.[4]
Distribution
Southwest BC south, west of the Cascades, and in Columbia River Gorge, to California.[3]
Habitat
Moist to well-drained soil, meadows and open woods, mostly west Cascades, Alaska to California, east to Alberta and northeast Oregon.[3]
Uses
Ecological: Adult Mardon Skippers (Polites mardon) feed on the nectar of R. occidentalis, among other flowers. [4]
First Nations: The juice from the flowers used as a poison. Seeds cooked and used as piñole either on their own or mixed with other seeds. The seed must be parched in order to remove an acrid principle.[5]
Seed
Seed sample from: 2011
Average Measurement: 3.5 x 2.6 x 1
Measurement Range: L: 3 - 4, W: 2 - 3, D: 0.75 - 1.25
Features
Shape: Seed surface is rounded, tapering off to a style that is opposite hilum, but off centered from it.
Additional structures: Style generally 1 – 2 mm long.
Color: Seeds are brown, tending toward a lighter brown or tan at edges of seed surface.
Surface: Seeds are papillose with some small ridges around the surface edges.
Latitudinal Cross Section: elliptical ![]()
Longitudinal Cross Section: elliptical ![]()
Basic Explanations and Assumptions:
The dimensions for the seeds are length x width x depth. The location of the hilum is used as the base of the seed, and the length is measured from hilum to the opposite apex. Where a style is present, the length is measured from the hilum to the bottom of the style. Width is measured at a right angle to the length at the widest part. Depth is measured at a right angle to the intersection of height and width lines.
Measurements included are the mean average for each measurement of ten separate seeds.
All measurements in millimeters unless otherwise noted.
Photo Gallery
References
- ↑ Integrated Taxonomic Information System. Retrieved from https://www.itis.gov/servlet/SingleRpt/SingleRpt?search_topic=TSN&search_value=18632#null
- ↑ WTU Herbarium, Burke Museum, & University of Washington. Retrieved from https://biology.burke.washington.edu/herbarium/imagecollection/taxon.php?Taxon=Ranunculus%20occidentalis%20var.%20occidentalis
- ↑ 3.0 3.1 3.2 Hitchcock, C. L., Cronquist, A., Giblin, D., & Legler, B. et al. (2018). Flora of the Pacific Northwest: an illustrated manual. Seattle: University of Washington Press.
- ↑ 4.0 4.1 4.2 Bowcutt, F., & Hamman, Sarah. (2016). Vascular plants of the South Sound prairies (First ed.). Olympia, Washington: The Evergreen State College Press.
- ↑ Native American Ethnobotany Database. Retrieved from http://naeb.brit.org/uses/search/?string=ranunculus+occidentalis